Chapter II: Physical Concepts
Table of Contents
- Chapter II: Physical Concepts
- What is temperature?
- LST from satellites
- How satellites see the surface?
What is temperature?
Following Norman and Becker, 1995, a "true" temperature would be measured with an arbitrarily accurate thermometer that makes a good thermal contact with the object of interest.
What is commonly referred to as air temperature, traditionally measured by an in situ thermometer in a shelter at 1.5 - 2 m height and with good contact with the air, corresponds to what is physically defined as a thermodynamic temperature. Generally thermodynamic temperature indicates the direction of the heat flow. It is defined by the second law of thermodynamics with absolute zero as the theoretical lowest value, the point at which the particle constituents of matter have zero motion and can become no colder. On the other hand, the faster these particles move, the higher the reading rendered by the measuring instrument. Thermodynamic and kinetic temperatures are often considered as equivalent but to be accurate the latter is actually a statistical interpretation of the former - kinetic temperature is a macroscopic quantity defined on a microscopic scale in terms of the mean kinetic energy of the particles (eq. 1):
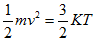
(eq.1)
Here m is the mass of a particle and v2 the mean square velocity of particles. K is Boltzmann's constant and T the kinetic temperature.
When retrieving land surface temperature by remote sensing technologies, namely using sensors onboard aircraft or satellite platforms, we are dealing with radiometric temperature, a subtle concept that presupposes the understanding of the nature of radiation and how it interacts with matter.
Sunshine is one of the most familiar forms of radiation which, broadly speaking, may be viewed either as electromagnetic waves or as a collection of radiation energy quanta called photons that propagate through space or matter.
According to Prevost's definitions, all objects at a temperature greater than absolute zero radiate energy and the quantity of energy emitted depends on the properties of the object and not on the properties or presence of neighbouring objects.
When radiation energy strikes an object, generally a part of the energy, Er, is reflected, a part Ea is absorbed and a part Et is transmitted through the object.
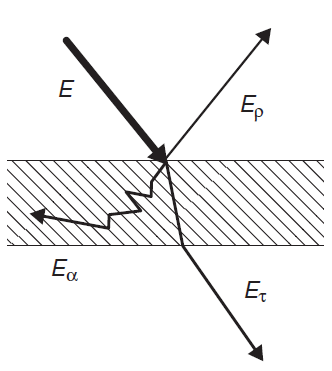
Since energy is conserved we have:
E = Er + Ea +Et (eq.2)
Defining reflectivity ρ, absorptivity α and transmissivity τ respectively as the ratios of Er, Ea and Et to the total incident energy, E, we obtain:
1 = ρ + α + τ (eq.3)
Kirchhoff created a thought experiment involving a radiative equilibrium between two totally opaque (i.e. τ ≡ 0 and therefore ρ = 1 - α) infinite parallel plates of different materials facing each other. The two plates, call them A and B , will be emitting and absorbing radiation. Let αA(λ,T) and αB(λ,T) denote the absortivities of plates A and B at wavelength λ and let the two plates to reach thermodynamic equilibrium at a common thermodynamic temperature T. Let MA(λ,T) and MB(λ,T) denote the emitted energy per unit time at wavelength λ by plates A and B at equilibrium temperature T. Kirchhoff demonstrated that the ratios of emitted energy to absorptivity have to be the same for all materials, i.e.
MA(λ,T) / αA(λ,T) = MB(λ,T) / αB(λ,T) = Bλ(T) (eq.4)
where Bλ(T) is a universal function. This function gives the emitted energy per unit time per unit wavelength of a totally opaque body in units of absorptivity (assuming zero reflectivity) for all wavelengths. Kirchhoff envisioned a material with zero reflectivity and coined the term blackbody to label it.
Radiation emitted by a blackbody in thermal equilibrium per unit time at a specific wavelength λ (μm) and temperature T (K) is given by Planck's law (eq. 5):
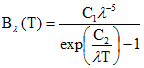
(eq.5)
The spectral blackbody radiance is given in units of Wm-2sr-1μm-1, λ is the wavelength in μm, c1 and c2 are the Planck constants (c1=1.19104x108 Wm-2sr-1μm4; c2=1.43877 x104 μm K).
However, real surfaces do not behave as blackbodies. The fraction of radiance emitted from a real surface compared to a blackbody at the same temperature is referred as emissivity. For instance, a surface with a known spectral emissivity of 0.96 would emit 4% less radiation than a blackbody at the same temperature. Surface emissivity at a given wavelength depends on vegetation type and density, soil moisture and soil chemical components. Emissivity is a property of the material but not independent of the angle of incidence: it is a directional variable. On the other hand, according to Kirchhoff's Law, for a given object emitting and absorbing thermal radiation in thermodynamic equilibrium, the emissivity is equal to the absorptivity.
Emissivity is very difficult to measure, and it represents the major source of uncertainty in land surface temperature measurements. For a Lambertian surface (isotropic emissivity and reflectivity), where the spectral emissivity is assumed to be known and assuming there is no atmosphere between the ground and the measuring sensor, the surface temperature may be obtained by simply inverting Planck's function (assuming that the emissivity is known):
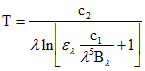
(eq.6)
As the temperature in eq. 6 is related to emitted radiation, it is referred to as radiometric temperature.
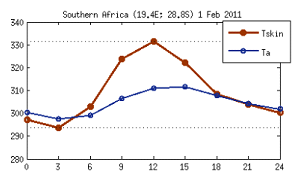
It is worth highlighting here that although radiometric and air temperature are different variables they are strongly correlated. However, they differ in phase and amplitude, as illustrated by fig. 2, which shows an example of a diurnal cycle over a given biome (savannah) for a particular date, taken from model data. It can be seen that the amplitude of Tskin is over 30 K (much higher than that of Tair) and peaks earlier than Tair due to the higher thermal capacity of the atmosphere (higher thermal inertia).
Fig. 2: Diurnal cycle of modelled Tskin and Tair over a given biome (savannah) for a particular date, showing the different phase and amplitude of these two variables.
For homogeneous isothermal surfaces, radiometric temperature is equivalent to thermodynamic temperature. However, land surfaces are not homogeneous, and so LST depends on within-pixel temperature and emissivity distribution, and is a directional quantity (Becker and Li, 1995).
As we have seen, the definition of radiometric temperature corresponds to the inversion of Planck's function, i.e, to a given radiance measured at a certain wavelength. Radiation is not monochromatic, however, but comprises a range of wavelengths. For the estimation of the surface energy budget in climate or numerical weather prediction models, we must consider the surface emitted radiation over the full infrared range, F, given by the integration of Planck's function for a gray body, i.e. a body where emissivity is the same for all wavelengths and directions,
F↑ = εσT4skin (eq.7)
This equation represents the so called Stefan-Boltzmann law, where σ= 5.67 x 10-8 W m2 K-4, and Tskin is called skin temperature.
The surface skin temperature can be derived from the energy balance equation:
(1 - α)S↓ + F↓ - (1 - ε)F↓ - F↑ - SH - LE - G = 0 (eq.8)
where α is the surface albedo, S↓ represents the downwelling shortwave radiation flux at the surface, F↓ is the longwave flux emitted by the atmosphere in downward direction towards the ground. ε is spectral averaged emissivity and (1 - ε)F↓ represents the portion of F↓ that is reflected backwards from the surface. LE and SH represent the surface latent and sensible heat fluxes, respectively, given by:
LE = coefE W (qskin-qair) (eq.9)
SH = coefH W (Taero-Tair) (eq.10)
coefE and coefH are bulk transfer coefficients for moisture and heat, W is wind speed, qskin is the saturated specific humidity at the aerodynamic temperature Taero (temperature at the height of roughness length for heat) and qair is the specific humidity at a reference level. Tair is the near surface air temperature (e.g. 2m shelter temperature). The radiometric (or skin) temperature is commonly used as a substitute for aerodynamic temperature in computing the sensible heat flux term SH in the energy balance.
So far we have clarified the physical meaning of radiometric temperature, the variable we are focusing on this product tutorial. We must also realize that due to its nature, radiometric temperature is not measured with thermometers (as thermodynamic temperature is), but with radiometers. Moreover, there is no direct method of measurement since what is being measured is emitted radiance and not radiometric temperature itself. Are the retrieving retrieval methods independent of the emitting surface?
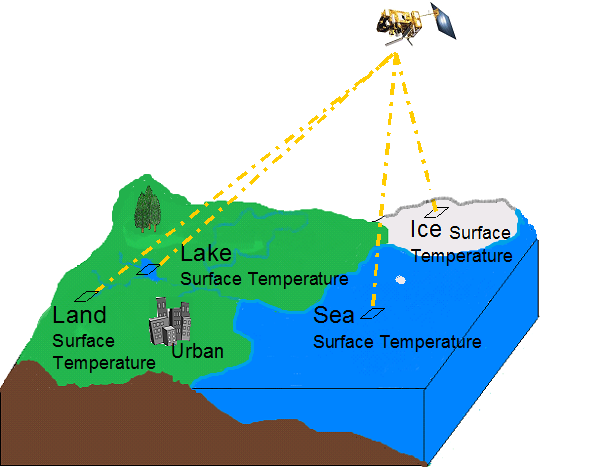
When we think about the surface of the Earth, in terms of its temperature, we need to take into account its different surfaces (land, lakes, ice, sea, urban, suburban), as illustrated in figure 3:
Fig. 3: This figure illustrates the distinct possible surface toppings. Adapted from: http://http://www.earthtemp.net
Although our focus here is on radiometric temperature, it should be noted that radiometric surface temperature signatures will vary according to the surface and its features. Land surface temperatures of different domains such as ice, sea and land are retrieved from remote sensing by applying different methods and algorithms. In this module we are focusing on one of these domains, the land.
LST from satellites
As mentioned before, if there was no atmosphere interposing between the ground (assumed as a Lambertian surface) and the sensor, and assuming the emissivity was known, the surface temperature could be obtained from the measured spectral radiance by inverting Planck's function.
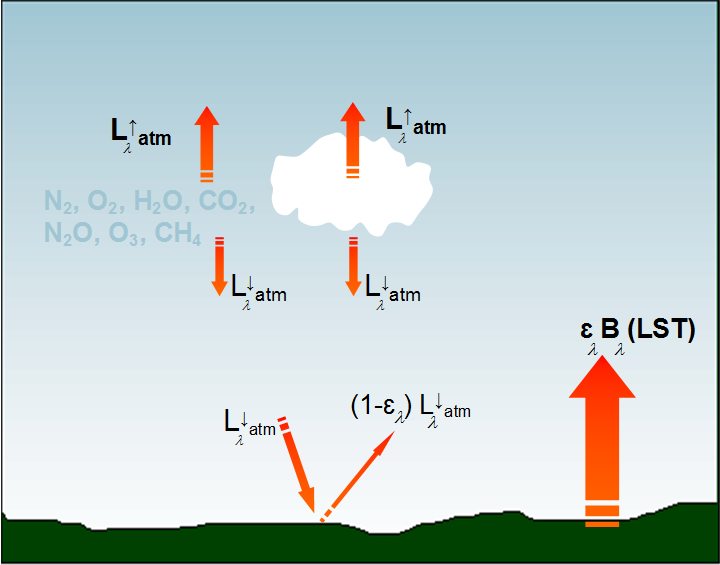
However, we cannot forget the layers composed of clouds, trace gases and aerosols that interfere with the propagation of radiation from the surface towards the top of the Atmosphere (TOA) by attenuating and re-emitting thermal infrared radiation. Figure 4 illustrates the several contributions to the OLR (Outgoing Longwave Radiation). OLR is the total energy emitted from the Earth and its atmosphere out to space in the form of thermal radiation. Most of it is emitted by the surface (Planck's law), followed by upward radiance emitted by atmospheric constituents (mainly water vapor) in the several layers of the atmosphere, L↑atm . This term varies strongly with the vertical structure of the atmosphere - warm/moist layers increase its contribution.
The atmosphere also emits longwave radiation downwards, which is then reflected back from the surface to the TOA (1 - ε) L↓λ atm (this term is very small, nearly zero for a spectral emissivity close to one).
Fig. 4: Contributions to the total outgoing longwave radiance reaching the top of the atmosphere (TOA): surface emission (Planck's law ελBλ(LST)) + upward radiance emitted by atmospheric constituents (mainly water vapor) in the different layers of the atmosphere, L↑atm + downward longwave radiation which is then reflected back from the surface to the TOA.
The actual longwave radiation reaching the TOA corresponds to the sum of all these terms multiplied by atmospheric transmittance (τλ) (aerosol absorption and scattering are considered to be negligible and are generally ignored (Prata et al 1995)):
Lλ = ελBλ(LST)τλ + L↑λatmτλ + (1-ελ)L↓λatmτλ (eq.11)
which is known as the Radiative Transfer Equation (RTE).
To summarize: Lλ is the total radiance we can measure by a satellite sensor at TOA and what we want to retrieve is LST. So in principle, if we had the information about the spectral surface emissivity and atmospheric composition, we could solve the RTE to get LST. This is assuming we have solved the issue of cloud masking, since LST from thermal infrared measurements can only be retrieved for clear sky pixels.
How satellites see the surface
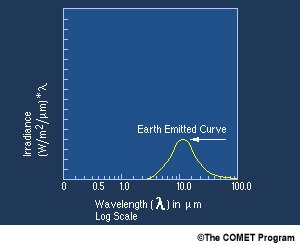
Computing Planck's radiation emission for an assumed average Earth temperature of 290 K as a function of wavelength, as shown in Fig. 5, leads to the conclusion that radiation emissions from the surface peak at around 10 μm, with 90% of total emission at wavelengths >4μm.
Fig. 5: Terrestrial radiation emission curve for an assumed average of 290 K.
As mentioned before, some atmospheric constituents (N2, O2, H2O, CO2, N2O, O3, CH4) interact with the propagating radiation in its path from the surface towards the satellite to a degree that depends on the concentration of these components, but also on the wavelength of the propagating radiation. Fortunately, there are some regions of the electromagnetic spectrum where these effects are less pronounced, which are called the atmospheric windows . Satellite sensors designed to sense the surface are equipped to make use of these windows.
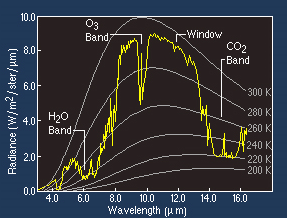
Fig. 6: Radiation emission curves for distinct surface temperatures ranging between 200 and 300 K computed with Planck's function. Observed radiation emitted from the surface at 295 K (yellow curve) is superimposed on top, revealing the attenuation effects of some atmospheric components (H2O, O3 and CO2).
Figure 6 shows surface emission considering different temperatures (200 K - 300 K) in the white curves, computed with Planck's function between 2 and 16 μm. The yellow line shows satellite-measured radiation values of the Earths's surface at 295 K. As observed, the yellow curve varies with wavelength due to absorption and emission by atmospheric gases at different pressure levels (O3, CO2 and mostly water vapor), revealing the presence of absorption bands as well as atmospheric windows where measured radiance is closer to the theoretical 300 K curve. As can be concluded from this figure, some atmospheric windows for thermal infrared radiation coincide with the spectral band where radiation emission from the surface is at its maximum. And yet, despite the atmosphere being almost transparent to thermal infrared radiation in the window regions, the effect of the trace gases is not negligible in the LST retrieval and therefore some correction is still required.
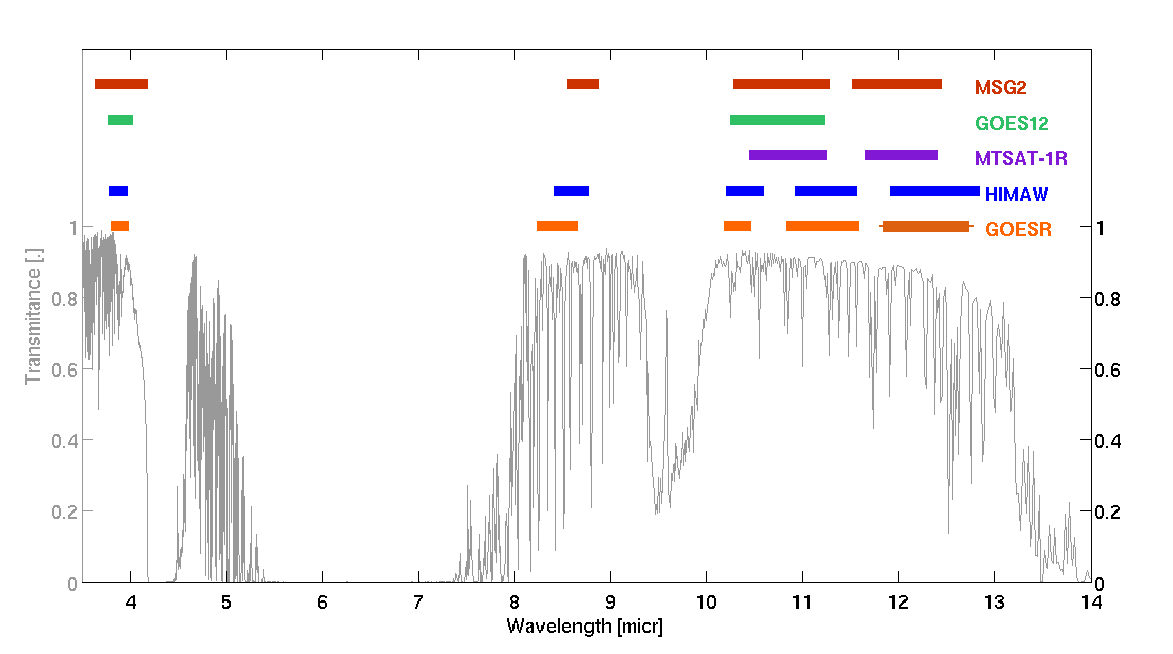
Fig. 7 shows the locations of some spectral channels that can potentially be used for LST retrieval. The atmospheric transmittance (gray line) is plotted between 3.5-14 μm. At the top of the figure are indicated infrared channels locations for 5 geostationary meteorological satellites, MSG, MTSAT, GOES12, GOESR and HIMAWARI-8.
Fig. 7: Atmospheric transmittance as a function of wavelength. Spectral range/location of thermal infrared channels for 5 geostationary satellites are indicated by the colored bars at the top of the graph.
We can see that in this set of satellites, the most recent ones (GOESR, HIMAWARI-8 and MSG) are fitted with 4 to 5 channels located in the thermal infrared windows.
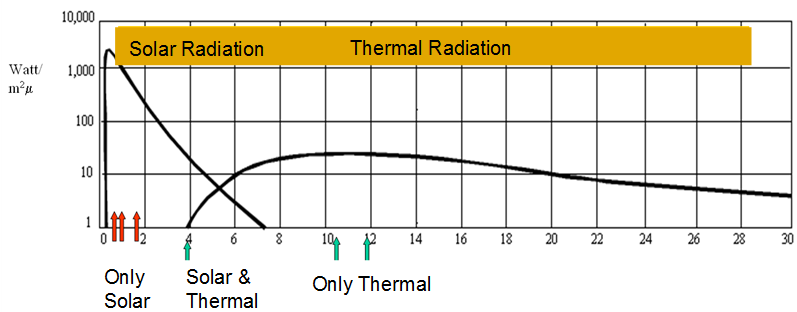
There are some issues with channels IR3.9 and IR 8.7 that hamper their use for LST retrieval. As seen in Fig. 7, IR3.9's transmissivity is close to 1 around these wavelengths, making it a good candidate (weak water vapor absorption in this band). Yet this channel is not only sensitive to infrared emission but also to solar reflected radiation, as shown in Figure 8. It is solar contamination of the IR3.9 channel during daytime that compromises its use for LST retrieval.
Fig. 8: This figure shows the solar and thermal emission curves as a function of wavelength. It is clear from these curves that the 3.9 μm channel is sensitive both to solar and thermal radiation, whereas the 8.7 μm, 10.8 μm and 12 μm spectral channels are only sensitive to thermal radiation.
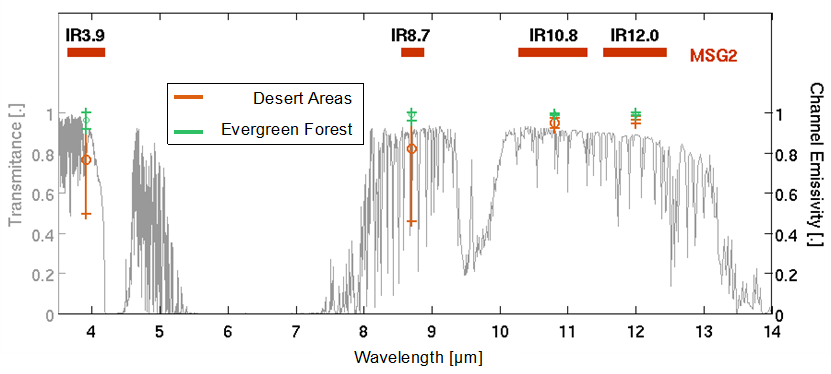
The second issue is related to the high variability of spectral emissivity both in IR 3.9 and IR 8.7 bands, particularly for desert areas. This can be seen in Figure 9, which shows atmospheric transmittance for the 3.5-14 μm range, this time superimposed with average and standard deviations of emissivity (right axes) computed from MSG2 IR channels for desert areas (in orange) and forests (in green). As can be seen, there is high uncertainty in emissivity estimations for both the IR3.9 and IR8.7 channels, mainly for desert areas.
Fig. 9: Atmospheric transmittance as a function of wavelength in the left axis. Spectral ranges/locations of thermal infrared channels for the MSG2 satellite are indicated by the red horizontal bars at the top of the graph. The average values and standard deviation of the emissivities computed from MSG2 channels 3.9 μm, 8.7 μm, 10.8 μm and 12 μm for deserts and vegetation are represented by the orange and green bars, respectively.
The remaining channels, IR10.8 and 12.0, are then the most commonly chosen candidates for satellite-based LST estimations. These channels are the most common choice since the atmospheric interference can be estimated from the difference in radiance between these two channels. On the other hand, these channels are also the ones where uncertainties in emissivity are relatively low for most types of surfaces.
But do we really need more than one spectral channel to estimate LST? What are the main obstacles for satellite-based LST retrieval?
Coming back to the RTE we see that even after taking into account the atmospheric effect (i.e. estimating the atmospheric transmissivity) we are still left with two unknowns in our equation: the spectral emissivity and LST. The problem is undetermined. As emissivity is a spectral quantity, even if we increase the number of channels (n >1), there will still be n+1 unknowns (n channels+LST). However, though there are ways to retrieve LST with a single satellite channel, the most common method uses several channels.
Given the fact that the inversion of the RTE is an ill-posed problem (there is no unique, well-defined solution for each choice of data) some assumptions and approximations must be made. Over the years several algorithms have been proposed for the many sensors in space working in the TIR (Thermal Infrared Region). In the next section a very brief overview on the different approaches is provided.