Meteorological Physical Background
Zonda events are the result of mountain-induced waves which produce downslope windstorms and turbulence. They have been widely studied with numerical models in the past, and several theories have been produced to explain them. Certain environmental conditions are favorable for the development of these waves, although it is important to note that given the complexity of the interactions among them, different combinations of parameters may lead to different results. However, the principal environmental features common to mountain wave formation are the following:
- A flow near-perpendicular to the mountain range at its top, with velocities above 15m/s.
- A stable layer near the top of the mountain range on the windward side.
- A "critical layer", that is, an upper layer where the flow is inverted.
- A low level pressure gradient that favours cross-mountain flow.
This mesoscale phenomenon is related to the proximity of a cold front accompanied by an upper-level trough, a strong cross-barrier mid-level flow, and depressions that cross the Andes further south.
| Spatial extent: | generally confined to the proximity of the mountains. |
| Duration: | sudden development, short duration (a few hours). |
| Intensity: | max winds = 50 km/h, gusts = 100 km/h in severe cases. |
Broad Overview
The three main physical mechanisms which generate high amplitude waves are:
- Hydraulic jump mechanism.
- High-amplitude vertically propagating mountain waves.
- High-amplitude breaking waves and self-induce critical-layers.
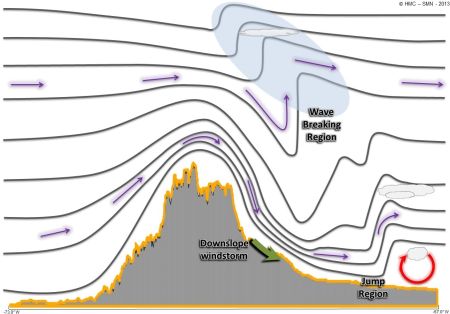
1. Hydraulic jump
This theory assumes the hydrostatic flow of a homogeneous fluid bounded by a free surface that passes over a barrier. This approximation leads to a balance between nonlinear advection, the pressure gradient forces caused by changes in the thickness of the fluid, and the gravitational force. It can be shown that the relative contribution of the first two terms can be quantified by using the Froude number (Fr2=U2/gD, where U is the fluid's velocity and D its thickness), and that advection always opposes the pressure gradient force.
If Fr>1 (supercritical flow), nonlinear advection is stronger than the pressure gradient force, and the balance is satisfied when the flow accelerates in the same direction as the gravitational force. This causes the fluid parcels to decelerate as they ascend, converting kinetic energy (KE) into potential energy (PE), and to accelerate as they descend, reconverting PE into KE.
If Fr<1 (subcritical flow), the pressure gradient term dominates, and the balance is satisfied when the fluid parcels accelerate in the direction opposite the gravitational force. That is, acceleration in the ascent - PE to KE as a result of the free surface drop - and deceleration in the descent - KE to PE.
If there is acceleration along the entire path overpassing the mountain,the air flow undergoes a transition from subcritical to supercritical, and very high downslope velocities are produced.This is achieved when there is enough acceleration during ascent; therefore the air flow eventually recovers the ambient downstream conditions.This turbulent process is called hydraulic jump. The high velocity is the result of a continuing conversion of potential energy into kinetic energy.
|
Schematic of: a) supercritical flow, b) subcritical flow and c) hydraulic jump. Adapted from Durran (1986).
|
2. Vertically propagating mountain waves
When the troposphere is divided into several layers with constant stability and wind shear within each layer, the small-amplitude hydrostatic waves may be partially reflected at the interfaces of the layers, resulting in the waves being amplified and when resonance is achieved windstorms down the slope occur. This energy reflection depends on the characteristics of each layer, although one of the most important features needed for generating high-amplitude waves and strong downslope winds is the presence of a stable layer near the top of the mountain range.
This method reproduces a more realistic environment than the hydraulic jump theory, and the observed data from radiosondes show directly when the conditions are favorable for the development of mountain waves.
3. High-amplitude breaking waves and self-induced critical layers
Another mechanism that can explain downslope windstorms is related to wave breaking and downward energy propagation.
The waves increase in amplitude considerably when there is an overturning in the streamlines (or isentropes). These statically unstable regions (in which potential temperature decreases as height increases) are characterized by strong turbulent mixing and a reversal of the wind's direction. The layer where this takes place is known as a "self-induced critical layer", and the energy of the wave remains trapped below it, creating a favorable environment for high-amplitude waves.
The existence of an environmental critical layer may also contribute to wave amplification, and it is a feature that can be diagnosed using radiosonde data.
This mechanism explains the clear air turbulence (CAT) above the mountains. It can also be applied in the case of high mountains, unlike the previous hydrostatic case, which is valid only for lower mountains.
|
Schematic of a mountain wave in the Andes showing the wave-breaking region and the similarity with a hydraulic jump.
|
Geographical Location
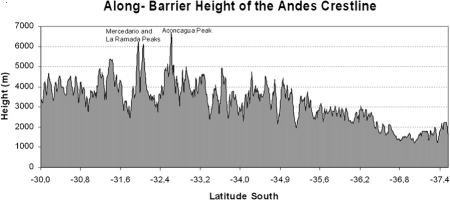
The extratropical Cordillera de los Andes runs meridionally from about 25°S to 37°S, with a variable width of 200-300 km and steep slopes on both sides. The height varies latitudinally, and the highest elevations are found around 32.5°S - 33.5°S, where the mean altitude is 4500 m; further south they get lower until the tops do not exceed 2500 m.
Zonda events are more intense where the mountains are higher and steeper. They occur more frequently between 35°S and 30°S, but the phenomena may extend further north up to 23°S. Further south, where the mountain range is considerably lower, zonda winds are rare events.
|
Latitudinal profile of the Andes between 30°S and 37.5°S. From Viale (2011).
|
Seasonal variety
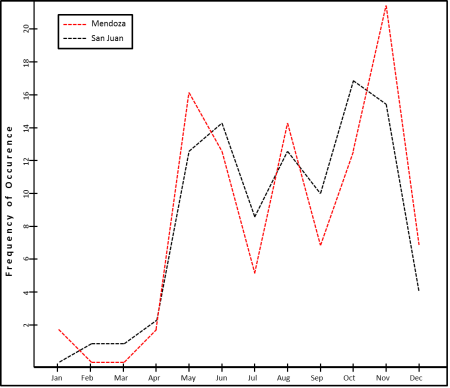
Zonda events are more frequent from May to November, when the conditions are more favorable for trough propagation towards lower latitudes, where the highest mountains are.
|
Monthly Zonda occurence frequency for San Juan (black) and Mendoza (red) stations. Adapted from G. Rolón (1977).
|