Meteorological Physical Background
There are two possibilities for air to flow past a mountain ridge. Either the air parcels go around the mountain or it is forced to rise over
the mountain: Which of these cases occurs, is dependent on several parameters:
The static stability (N), the height of the mountain or mountain ridge (h) and the wind component perpendicular to the mountain (U). The term
Nh/U combining these parameters gives an idea whether there is a flow across the mountain or not: If U is small the mountain is difficult to
cross; also if N increases (i.e. the atmosphere becomes more stable) the mountain will be more difficult to cross.
But even in the case of air partially streaming around the mountain, those streamlines approaching a greater height will cross the mountains.
When the wind has a component perpendicular to a mountain chain the air accumulation due to deceleration of wind speed by the obstacle on the upwind side creates high pressure. Part of the air is deflected upward giving rise to mountain waves. According to the theory of internal gravity waves, an air parcel within a stable stratified atmosphere will start to oscillate, as long as the waves are damped by friction.
Waves can only occur in a stable atmosphere. An air parcel which is removed from its original place cannot oscillate if there is no returning force. Lee Cloudiness will form where there is a sufficient supply of humidity near the wave crests and where there is upward motion. In the regions with downward motion the clouds will evaporate. The result is the pattern of parallel cloud lines perpendicular to the mountains.
One parameter to describe the state of the atmosphere in this situation is the Brunt - Vaisala frequency N2 which is defined by the following equation:

where
| T | temperature |
| θ | potential vorticity |
| g | gravity constant |
| cp | specific heat at constant pressure |
| N2>0 | stable atmosphere |
| N2 = 0.02 -0.03 | inversions |
| N2 = 0 | neutral atmosphere |
Another important parameter is the Scorer parameter (symbolised by I) which combines stability and characteristics of the wind field; it is approximated by following equation:

where
| U(z) | profile of the wind speed on the windward side of the mountains |
| N(z) | Brunt-Vaisala frequency |
The typical profile of the Scorer parameter shows a high gradient in low levels due to increasing wind speeds. Higher levels often show values of about 0.0005/m, rarely exceeding 0.001/m. The smaller the Scorer parameter the easier Lee waves are formed.
This parameter and the dimension of the mountain (L) determine if Lee Waves can be formed. The broader the mountain the easier waves can be formed. This relation can be expressed (assuming N and U are constant with height) by:

Indicating that no Lee Waves are formed, but perturbations which decrease with height.

Lee Waves are formed.
The dimension of a critical width (L) is several kilometres, increasing with wind speed, but decreasing with increasing stability. If a mountain is not wide enough, Lee Waves will not develop.
Lee Waves are a form of vertical energy propagation. At higher levels the density of the air is less, which means the amplitude has to increase. Therefore the wavelength increases with height, which clearly is reflected in the more extended area of High Lee Cloudiness.
The wavelengths also depend on the shape of the mountains. There often is a dominating wave length.
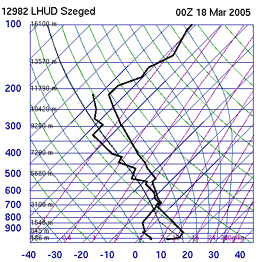
The example from 18 March 2005 shows some of the parameters mentioned above. The image shows a region with Lee Cloudiness extending from the South Alps to Hungary, Slovenia and Croatia. The nearest available radio sounding was Szeged which is indicated on the image. The Lee Cloud is quite high in this case and can be found just below 300 hPa.
|
18 March 2005/06.00 UTC - Meteosat 8 IR10.8 image
|
18 March 2005/00.00 UTC - radio sounding Szeged
|
The air column over Szeged shows a stable layer restricted by an inversion around 700 hPa. The Lee Cloudiness under consideration is within a stable layer. This is in agreement with the above mentioned statement that Lee Cloud can only develop in a stable atmosphere.
Trapped Lee Waves
A special class of Lee Waves are called "Trapped Lee Waves". This phenomenon is characterised by waves only occurring at lower levels. They occur when the vertical distribution of the Scorer-parameter can be approximated by two levels: an upper level with a quite low value for I(z), (due to the increase of wind speed and the decrease of the Brunt - Vaisala- frequency) and a lower level with a much higher value for I(z). In some cases (depending on the mountain range) the upper atmosphere cannot form waves, but the lower levels can. So the waves are trapped in this lower layer. In satellite imagery the height of the Lee Wave varies significantly from case to case. The trapped Lee Wave theory might be an explanation for apparently low cloud tops.
Sometimes in the lee of the mountains one can find inversions or at least strong stability near the surface and quite strong winds above it. Waves are found in these layers. In these situations displacements are large, which might result in a breaking of the waves.
N - S oriented mountain chain
If the N. - S. extent of a mountain range is large, effects of earth rotation are no longer negligible. As a consequence the flow over the mountain is no longer symmetrical. Due to changes in wind speed during ascent there is a changing in the strength of the Coriolis force. When a westerly flow passes a long mountain range extending north to south (e.g. the Scandinavian mountains) there will tend to be higher wind speeds to the south and lower wind speeds to the north.
Determination of Wind speed
The wind direction is quite similar at all levels but the wind speed increases with height. The typical wind speed lies between 10 and 20 m/s at the 700 hPa level, between 15 and 25m/s at the 500 hPa level and 15 to 35 m/s at the 300 hPa level. In literature it is said that - depending on the shape and scale of the mountain chain - the maximum wind is either found at the top of the mountain ridge or at the leeward side. Since ECMWF data were used in the study made by ZAMG, no change in the wind field by the mountains can be seen (restriction due to resolution).
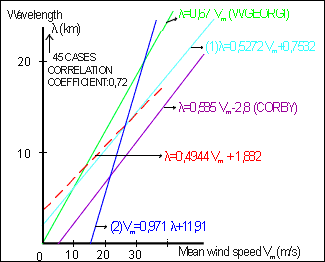
There is a connection between mean wind speed and wave length of Lee Waves, although with rather a low coefficient of correlation. It can be approximated by a linear function (the higher the wind speed the longer the waves). However, such a linear regression is only valid for a certain indicated area.
The above figure shows the correlation between mean wind speed and Lee Wave length (Cruette, 1976).
The straight lines symbolise different linear regressions found by several authors for different regions.
Unsolved problems
There are some unsolved questions relating to Lee Cloudiness which is discussed below:
Lee Cloud exceeds the mountain ridge line
There are cases which give the impression that Lee Cloudiness is more extensive than suggested by the orography. This can even lead to apparent "Lee Cloudiness" over the sea.
|
22 March 2007/12.00 UTC - Meteosat 8 IR10.8 image
|
|
This effect is sometimes observed east of Iceland but it is difficult to find an explanation.
Cloud stripes parallel to the wind direction
There are sometimes cloud stripes aligned parallel to the wind direction. They look like waves, but they are, in fact, perpendicular to the typical direction of Lee Waves.
There are some possible explanations:
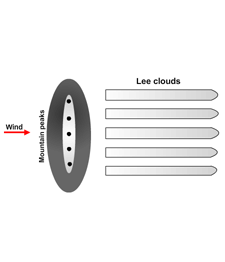
The single lee bands are generated separately by each mountain, so the cloudiness follows the orography (as shown below). Arguments in favour are:
- The stripes usually occur at the same location.
- These stripes seem to be partially developed Lee Cloudiness, i.e. the airflow over the mountain range does not show wave characteristic over the whole length of the chain but only over some specific locations favoured.
|
|
03 November 2006/12.00 UTC - Meteosat 8 HRVIS image; green: wind vectors 850 hPa
|