Low-level wind over flat terrain is mainly influenced by the pressure gradient force and by friction. In the case where an obstacle like a mountain range hampers the propagation of the air, the airflow has two possibilities: either to flow over it or to split and circle around both sides of the obstacle. While the overflowing wind is hardly decelerated, the airflow that diverts around the mountain range is decelerated and partly blocked at the windward side of the mountains. This decelerated area continuously expands upstream over time (see Figure 1).
Figure 1: Flow from the north against the Alps. Blue arrows show the deflected air streams, the red arrow shows the overpassing air stream.
The behaviour of the flow largely depends on two factors: atmospheric stability and wind speed. The Froude number (here in a non-classical form) describes the behaviour of an air flow hitting an obstacle:
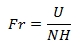
where U is the mean wind speed [m s-1], H is the height of the barrier [m] relative to the height of the air stream and N the Brunt-Väisälä frequency [s-1].
The Brunt-Väisälä frequency represents the vertical static stability of the air mass. For a Froude number Fr >> 1, the air tends to flow over the obstacle, and in the opposite case (Fr << 1) it tends to flow around the obstacle.
So far, we have only considered an ideal case where the airflow takes one of the two possibilities. In reality, we usually find both kinds of flow behaviour. In the lower levels, the wind needs more kinetic energy to crest the mountain than in levels slightly below the mountaintop. Lower winds are therefore either blocked or deflected around the obstacle, while higher up winds tend to pass over the mountain peaks. Typically, the wind will prefer to pass over the lowest ridge elevations, which in turn leads to a channelling effect that can be observed at many mountain passes in the Alps.
A low-level airflow from the north that is encountering an obstacle is partially blocked on its way south before it is either lifted and overflows the Alps or contours (moves around) them. Blocking leads to an upwind pressure rise near the ground and to a pressure drop at the leeward side of the mountains, which is caused by the isentropic (constant entropy) heating of the downward flowing air that overcame the obstacle (see Figure 2).
Figure 2: Mean sea level pressure and IR10.8 μm image from January 5, 2019 at 12:00 UTC. Orographic blocking of cold air from the north leads to a large cross-Alpine pressure gradient.
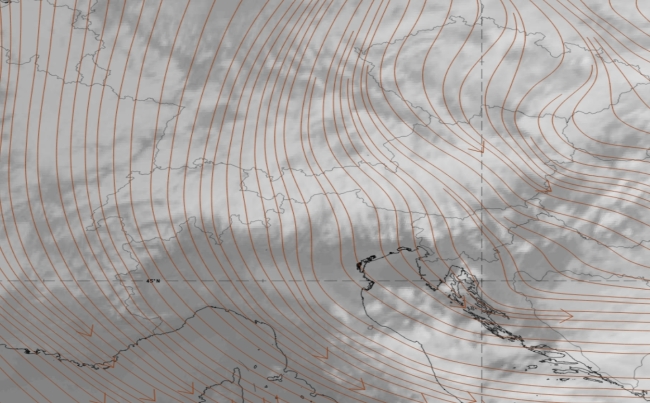
For air aloft (e.g., above 700 hPa for the Alps) that overpasses the mountain range without being deflected around the mountain range, we observe a "strange" behaviour of the flow of the air current. The trajectory is reflected in the undulated shape of the isolines of the geopotential height (see Figure 3).
|
|
Figure 3: Geopotential height and streamlines at 500 on IR10.8 μm image from January 2, 2019 at 12:00 UTC. Use the sider to compare both images.
So why is it that the overflowing air is first deviated to the west and then back to the east as demonstrated in the example above? To better understand this behaviour, we have to investigate the vorticity of such an air parcel that is lifted over the Alps. In fact, we will use the concept of the potential vorticity (PV) as this dimension is preserved when air parcels move along isentropic surfaces. Air parcels usually move along isentropic surfaces at higher atmospheric levels, assuming that diabatic heat exchange and turbulent mixing are neglected.
Potential vorticity is the absolute vorticity of an air parcel moving along an isentropic surface. Note from the relation below, that PV is simply the product of absolute vorticity on an isentropic surface (ζθ + f) and static stability (∂θ/∂p). Hence, PV consists of two factors, a dynamic and a thermodynamic part:

When air moves along isentropic surfaces (no diabatic heating, no turbulence or friction), we can state that:
PV = constant
for any air parcel in the upper troposphere.
Under stable conditions, isentropic surfaces are closer to each other than under unstable conditions. This is the case near the tropopause, where the atmosphere is very stable. When static stability decreases, for example when air moves to lower atmospheric levels with less stability, vorticity increases because absolute vorticity and static stability are coupled due to the conservation of PV.
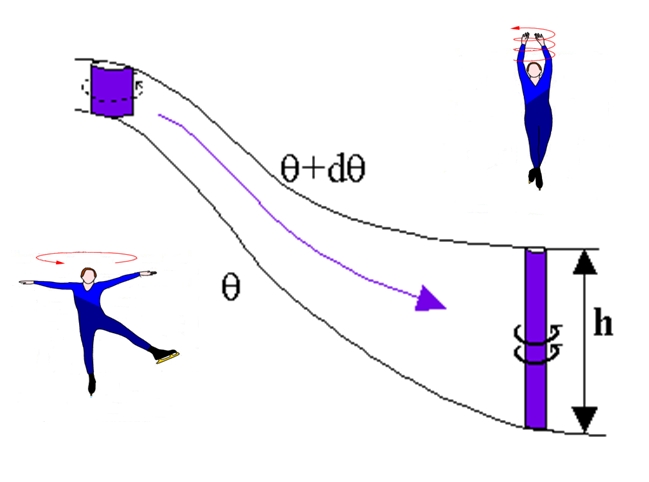
To give a more pictorial explanation, imagine an ice skater outstretching their arms while spinning and then raising them. Their vorticity (rotating speed) increases the more they stretch their body. This figure can be applied to an air column that is stretched while it moves into a less stable region (see Figure 4).
Figure 4: Illustration on how rotation (vorticity) increases when the air column is stretched.
Now let's apply this concept to air that passes over a mountain range. We assume for simplicity that the Coriolis parameter f is constant whether the flow crosses a north to south or an east to west oriented mountain range.
Figure 5: Cyclogenesis at the lee of the Alps. (a) Vertical cross section and (b) a map of the airflow (view from above).
A → B
When the air parcel approaches the mountain range, the air column is slightly stretched because the distance between the isentropic layers θ0 and θ0+Δθ becomes larger. In order to conserve PV when static stability ∂θ/∂p decreases, relative vorticity must increase. The airflow turns left (in the northern hemisphere).
B → C
Closer to the mountain range, the air at lower levels is lifted much more than the air at higher levels. The air parcel is compressed and static stability increases because isentropic surfaces are closer to each other. Vorticity decreases, the flow becomes anticyclonic and turns right (in the northern hemisphere).
C → D
After passing the mountain crest, the air column is stretched again, vorticity increases and the flow becomes more cyclonic. This coincides locally with the surface pressure minimum at the lee side of the mountain range. On the other hand, stability decreases which often leads to convection on the lee side, especially during the summer season.
D → E
Finally, the air parcel comes back to its initial vertical extension; static stability and absolute vorticity are the same as before the mountain crossing.