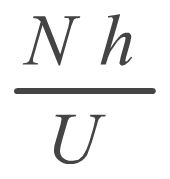Topography
The effect of topography in the spread of fire is a very complex issue because topography itself is complex. Each case will always be an individual case and generalizations may be misleading. Nevertheless, based on experience, experiments and numerical simulations, one can state that in general:
- The rate of fire spread is higher in upwind slopes than in downwind slopes.
- Steeper slopes cause higher fire spread rates.
The effect of slope on fire spread can be seen in the following animation. When the angle between the flames and the fuel is decreased, the effect is pretty much like the effect of wind on flames. If, additionally, there is wind on a slope, then the rate of spread increases dramatically.
Results obtained from experiments on the variation of fire spread with slope can be plotted in graphics (see Figures 3.6 and 3.7).
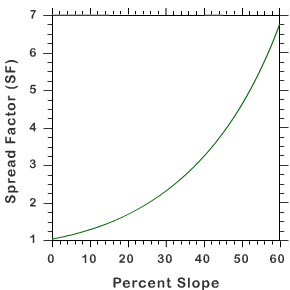
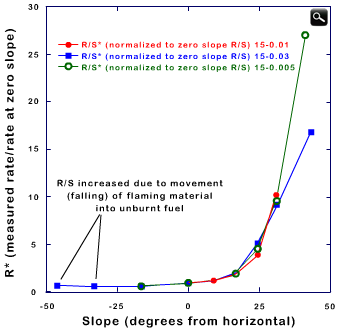
The graphics show that a fire propagates faster upslope if a terrain is steeper and that the spread increases dramatically for slopes greater than 10�. However, it also shows that the behaviour is quite different for a downslope fire propagation (negative values of slope):
- Fire spread has very low values!
- There is not too much impact of slope!
In fact, when a fire reaches the top of a hill, an increase in the fire spread rate is expected as winds are strongest there. However, when the fire advances to the lee side on the hill and starts to propagate downslope, there is a strong decrease on fire spread rate. This happens, not only because of the effect of (down)slope, but also because winds are weaker in the lee side (Forthofer, 2007).
Now consider the flow over a mountain ridge. Numerically this flow can be parameterized by the inverse Froude number:
where N is the Brunt-V�is�l� frequency, h the mountain height and U the wind speed.
Take also into account that if wind speed U is kept constant, this will result in a steeper mountain as Nh/U increases.
In numerical experiments (eg. Olafsson and Bougeault, 1996) it was found that for Nh/U > 1.4 (therefore for steeper mountains) most of the air mass that meets the mountain is decelerated and partly reversed (Figures 3.8 and 3.9).
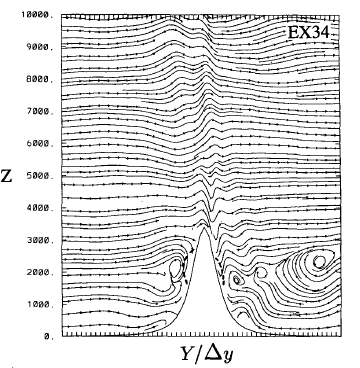
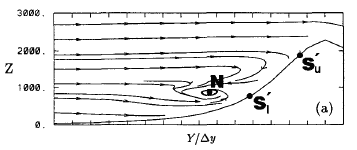
In fact, when there is an upstream blocking, streamlines computed in the numerical experiments clearly show the formation of vortices and the split of the flow in two parts: one part of the flow ascends the mountain and the other part returns and flows down the upstream slope.
Fig 3.10 - Gentle slope - the fire propagates faster up to the top of the mountain.
Fig 3.11 - The slope increases, the flow becomes turbulent and the down-slope wind of the vortices may slow down the propagation of fire up-slope
You can see that although many studies show that the upstream fire spread rate increases with increasing slope, you also have to take into account that rougher topographies may produce a change in the flow regime and lead to the creation of vortices and a reversal of the flow!
In fact, other studies stress that wind variability has a greater impact on the rate of fire spread rather than wind speed (Carrega and Fox, 2006). In particular, experiments show that at high wind speeds, a very turbulent wind creates a lower fire rate of spread!
So, now you can understand why fighting fires in mountains can be so difficult - there are some rules, but topography will always reserve a veto! In fact, there are numerical models that try to reproduce in detail the spatial spread of a fire through a specific topography (see Figures 3.12 and 3.13).
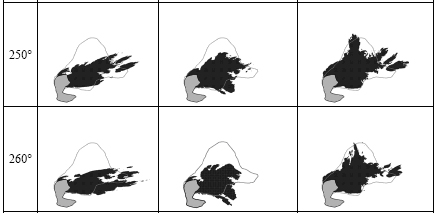
Question
Now that you have read through many factors that contribute to the risk of fire, you may wonder how experts try to combine all the information.
The correct answer is B.
To explain the answer briefly: the first option is still currently in use, but one has to be able to interpret different kinds of information.
The second option is the correct option. For firefighting purposes a single index is the most desirable in an early stage, with the possibility of going deeper into detail if needed! One example of a single index is the Canadian Fire Weather Index, or FWI. You will learn more about this index in the next slides.
Finally, the last option is incorrect. Black box schemes are never desirable!