Meteorological Physical Background
Although more physical parameters (e.g., IPV) could be used for the dignosis of summer convection we will concentrate upon the relevant parameters of the case study.- Dynamical forcings (Vorticity and Vorticity advection, Tendency, Omega)
- Potential instability and KO-index
- Pseudopotential temperature
- Conceptual model of a super cell
- V-notch
Which of these theories can be applied to this case study?
Ad1. Cyclogenesis according to the classical polar front theory
For more detailed background (e.g., derivation of equations) see for example: Holton, James R. An introduction to dynamic meteorology / 3rd edition, 1992 / ISBN 0-12-354355-X. In the following only the rules for the practical application will be given. It should be pointed out that the so-called quasi-geostrophic theory is applicable for structures in the synoptic and mesoscale domain (e.g., surface low and highs, upper air troughs and ridges, frontal bands). However, this theory can help us to indentify synoptic weather situations likely for developing of summer convection in relation to dynamical processes, e.g. for the „earliy warning" in the nowcasting process.
i. Vorticity and Vorticity advection
For the synoptic and mesoscale domain the relevant contributions to the vorticity are the shear vorticity and the curvature vorticity. We get a positive (negative) contribution in the case of a) decreasing (increasing) wind speed normal to the wind direction and b) turning of the wind counter-clockwise (clockwise). We have increasing vorticity when positive vorticity is advected and horizontal divergence happens. Sometimes super cells are connected to mesocyclones (radius about 10 km). In this case also the twisting term and the vertical advection of vorticity are important. In the diagram below the principle of the twisting term is explained (Topic 4).
Typicaly, we observe for waves length of less than about 3000 km positive (negative) vorticity advection at the front (rear) side of an upper air trough axis and at a left (right) exit or right (left) entrance region of a jet streak.
ii. Tendency-equation
It is possible to derive the geopotential tendency equation from the vorticity equation and the equation for the thickness of a hydrostatic atmosphere. We have decreasing (increasing) pressure tendencies in the case of positive (negative) vorticity advection. That means that west of the axis of an upper air trough we have negative pressure tendencies and east of this axis positive pressure tendencies. The second factor is the rate of change of temperature advection with height. If the warm air advection increases (decreases) with height we get negative (positive) tendencies.
iii. Omega-equation
The Omega equation can also be derived from the vorticity equation and the equation of the thickness of a hydrostatic atmosphere followed by some mathematical operations (see for example: Holton, 1992). The differential advection of vorticity and the advection of thickness within a hydrostatic atmosphere (i.e. thermal advection) are relevant for the vertical motion. We have an upward (downward) motion in the case of an increase (decrease) of vorticity advection. That means that we observe an upward (downward) motion above a surface low (high) and at front (rear) side of an upper air trough.
Warm (cold) air advection causes an upward (downward) motion. We observe east of the warm front the most intense upward motion and rear of the cold front downward motion.
The patterns of thermal and vorticity advection may neutralize each other more or less. However, if we have both positive vorticity advection and warm air advection intense upward motion and strong negative pressure tendencies (i.e. cyclogenesis and/or intensification of fronts) occur.
Ad 2. Potential instability and KO-Index
Potential instabil means that only in the case of an upward motion a destabilisation of the atmosphere and convection occur. There exist many indices to forecast the intensity of convection. In this case study we use only NWP-fields of the KO-index. In the KO-Index the potential equivalent temperature (Θa) at 1000, 850, 700 and 500 hPa are considered.
The KO-Index is defined as:

Θa is the temperature after condensation of all water water vapour without changing the pressure at one particular level. The air package gets all condensation energy and is moved afterwards to 1000 hPa. During stable situations Θa is increasing with height. For a potential unstable air mass we get a decrease. The formular indicated that negative values are related to a decrease of Θa between lower and middle altitudes.
The following thresholds are being used: KO > 6: no thunderstorms, 6 = KO = 2: thunderstorms possible, KO < 2: thunderstorms likely
Ad. 3 Pseudopotential temperature
The pseudopotential temperature (tpspot) is a combination of the air temperature and the humidity. Tpspot is the temperature that an air mass package will have after condensation and falling out of all water vapour due to upward motion followed by dry adiabatic downward motion to the starting position. In practise the combination of tpspot and the wind barbs should be used. If we have a convergence in an area with relatively high tpspot we should be aware to convection or even severe thunderstorms.
Although we have that parameter only for 2m-values the following thresholds can be used as guidlines: tpspot < 50°C: thunderstorms not likely, 50 ≤ tpospot < 60: thunderstorms possible, 60 ≤ tpspot < 70: thunderstorms likely (partly severe), 70 ≤ tpspot < 80: severe thunderstorms, tpsopot > 80: extreme thunderstorms
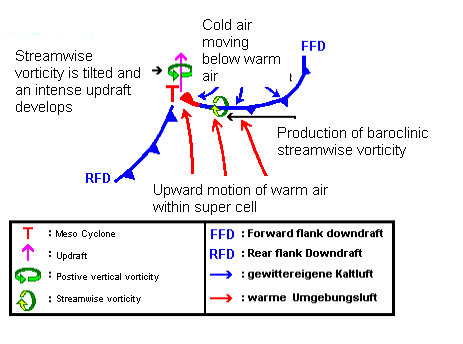
Ad 4. Conceptual model of a super cell
The following characteristics of a super can be found:
- Most dangerious convective phenomena in Middle Europe
- Diameter: 20 to 50 kilometres (low levels), over 100 kilometres at the top
- Big areas of clouds extending to the tropopause
- Overshootings (below -60°C)
- Fast upward and spatial growing (i.e., fast decreasing of temperature and increasing of areas with cold cloud tops)
- Life time often 6 hours, partly up to 12 hours
- Often hail, heavy precipitation and strong gusts.
We assume that the synoptic preconditions (vertical wind shear, potential instability, dynamical forcings) are fulfilled. In the following the main features of a super cell will be explained.

|
 Schematic cross section through a super cell with hail and relative wind. The super cell is moving from left to right. In the lower levels we oberserve a streaming into the super cell whereas in the higher levels an outward streaming happens. Due to the baroclinic situation the updraft is tilted yielding hail. We observe hail behind the gust clouds and a few kilometres after the passage of the gust front. In some cases hail is also possible several kilometres before the super cell. After the onset of hail the downdraft arrives the location with prevailing moderate to severe rain. At the top of the updraft overshooting is likely.
Schematic cross section through a super cell with hail and relative wind. The super cell is moving from left to right. In the lower levels we oberserve a streaming into the super cell whereas in the higher levels an outward streaming happens. Due to the baroclinic situation the updraft is tilted yielding hail. We observe hail behind the gust clouds and a few kilometres after the passage of the gust front. In some cases hail is also possible several kilometres before the super cell. After the onset of hail the downdraft arrives the location with prevailing moderate to severe rain. At the top of the updraft overshooting is likely.
For detailed information please see: IC 5.7: Convective Storm Structure and Evolution
Ad 5. V-Notch
A V-shaped notch is on the leading edge of a super cell and caused by the divergence of an intense updraft. The peak of the „V" is directed to the direction of the upper stream. The following two diagrams show the shape of an V-Notch. A V-Notch is a clear hint to severe thunderstorms with heavy rain, hail strong gusts (often up to Beaufort 12).

|
Cross section, top view and GOES-IR 10.7 μm of a V-Notch . |

|
Model trajectories of a V-Notch (Scott Bachmeier, University of Wisconsin) . |
Additional information